Prethodno poglavlje | Pocetna strana | Sledece poglavlje

4. DINAMIKA ROBOTA

Dinamika robota je od svih teorijskih aspekata robotike poslednja nasla praktičnu primenu. Zato ćemo na početku izneti određena obrazloženja i argumente u prilog njene primene.Krenimo od činjenice da se uspešno projektovanje i upravljenje nekog sistema ne može izvesti bez njegovog dobrog poznavanja. Ovo je, svakako tačno, ali pod pojmom "dobrog poznavanja" ne podrazumeva se uvek isto. Razmatrajmo problem mehaničkog sistema - konkretno jednog robota. Dobro poznavanje takvog sistema može, a ne mora uključivati poznavanje matematičkog modela njegove dinamike (tzv. dinamičkog modela). U ranijim fazama razvoja robotike projektovanje robota nije uključivalo tačan proračun dinamike, a upravljanje nije vodilo računa o mnogim dinamičkim efektima već se, uz određene aproksimacije, svodilo na poznatu teoriju automatskog upravljanja. Ovakav pristup bio je posledica nerazvijene teorije robotike. Naime, dugo vremena praksa proizvodnje i primene robota razvijala se nezavisno od teorije koja je bila često isuviše akademski orijenti-sana. Ovakvo stanje ipak nije sprečilo neke proizvođače da naprave veoma uspešne robotske uređaje.U današnje vreme, međutim, zahtevi za složenim i vrlo brzim robotskim sistemima diktirali su povezivanje teorije i prakse. Sa stanovišta primene dinamike robota ključnu ulogu je odigrao razvoj efikasnih metoda za proračun dinamike uz pomoć računara. Uz niz kasnije razrađenih metoda, dinamički model i na njemu zasnovani proračuni i simulacija, postao je nezaobilazni deo svakog uspešnog pro-jektovanja robota.Druga mogućnost za primenu dinamičkog modela je dinamičko upravljanje. Ta mogućnost se danas još uvek malo koristi, međutim, metode za sračunavanje dinamike u realnom vremenu, koje već postoje, znatno nas približavaju ovom cilju.Ova glava razmatra prvo osnovni pristup opisivanju dinamike robota i formiranju dinamičkog modela. Detaljno izvođenje jedne od metoda za formiranje modela dato je u prilogu P3, a ovde se razmatra forma i korisćenje dobijenog rezultata. Ovo je urađeno zato da bi se ova glava rasteretila od dugačkih matematičkih izvođenja koja zahtevaju i obimno znanje mehanike.Dalje u ovoj glavi se razmatra rešavanje direktnog i inverznog problema dinamike, a zatim i primena računara u proračunu dinamike robota. Na kraju ćemo ukazati i na neke specijelne probleme: dinamika robota sa elastičnim deformacijma u sistemu za prenos pogona i dinamika u fazi funkcionalno zatvorenog lanca.

4.1. DINAMIČKI MODEL ROBOTA

Pod dinamičkim modelom robota podrazumevaćemo sistem diferencijalnih jednačina koje opisuju dinamiku robota.   Izvođenje modela zahteva dosta znanja iz mehanike, pogotovo mehanike krutog tela, koje veći broj čitalaca možda nema. Zato ćemo ovde izložiti glavne ideje i formule i interpretirati krajnji rezultat, a detaljno izvođenje modela dati u prilogu P3.

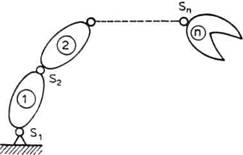
Sl. 4.1. Robot kao otvoreni kinematički lanac

Posmatrajmo manipulacioni robot kao otvoreni kinematički lanac bez grananja (sl. 4.1). Označimo zglobove redom sa S₁, S₂,..., Sna segmente sa 1,2,...n. Pretpostavimo, zatim, da su zglobovi takvi da omogućavaju jednu relativnu rotaciju ili jednu relativnu translaciju. Kako svaki zglob ima po jedan stepen slobode to će mehanizam ukupno imati n stepeni slobode. Dinamiku takvog mehaničkog sistema možemo opisati sa najmanje n skalarnih diferencijalnih jednačina drugog reda. Taj sistem jednačina zvaćemo dinamički model.  

U glavi 2. posvećenoj kinematici uvedene su tzv. generalisane koordinate q₁,..., q_n kao najmanji skup parametara koji jednoznačno definišu položaj robota.Za generalisane koordinate izabrana su pomeranja u zglobovima pa smo ih zvali i unutrašnje koordinate. Vektor unutrašnjih (generalisanih) koordinata je definisan kao

Dinamiku mehanizama robota možemo sada opisati na više načina: primenom opštih teorema dinamike sistema (teorema o količini kretanja i teorema o kinetičkom momentu), primenom Lagranževih jednačina, primenom Apelovih jednačina ili Gausovog principa. Model koji se dobija svakako je isti bez obzira nai pristup koji se koristi jer su svi ovi pristupi u suštini ekvivalentni. Međutim, sa stanovišta metodologije sastavljanja modela razlike su bitne. Ovde ćemo koristiti; opšte teoreme dinamike jer takav pristup zahteva najmanje znanja iz mehanike. Da bismo formirali dinamički model celog sistema tj. celog lančanog mehanizma krenućemo od posmatranja jednog njegovog segmenta. Neka to bude segment "j". Ako hoćemo da posmatramo segment izdvojen, napravićemo zamišljene prekide lanca u zglobovima i  (sl. 4.2). Na slici 4.2a prikazan je prekid u zglobu . Međusobno dejstvo segmenata pokazuje se u obliku parova sila i momenata, dakle u obliku akcija i reakcija. Ako pod akcijom podrazumevamo dejstvo narednog segmenta (j) na prethodni (j-1) onda pod reakcijom podrazumevamo dejstvo prethodnog na naredni. Tako, i bi predstavljali reakcije, a  i  akcije. Sila  momenat  nekada se nazivaju ukupnom silom i momentom u zglobu jer predstavljaju ukupno dejstvo koje se kroz zglob prenosi sa prethodnog segmenta na naredni.

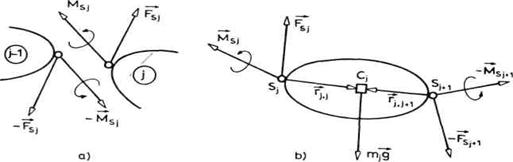
Sl. 4.2. Izdvajanje jednog segmenta lanca

Ako sada izdvojimo segment "j", na njega će delovati sile i momenti kako je prikazano na slici 4.2b. Treba naglasiti da se u sili  i momentusadrži i pogon koji u tom zglobu deluje. Ako je posmatrani zglob translatorni, tada se pogonska silasadrži u sili , a ako je zglob rotacioni, tada saoznačavamo pogonski momenat i on se sadrži u momentu . Treba naglasiti da je u pitanju takozvana izlazna sila ili izlazni momenat pogonskog motora, a ako postoji reduktor, onda se radi o izlaznom momentu reduktora. Opišimo sada kretanje izdvojenog segmenta "j". Pomeranje težišta segmenta opisujemo takozvanom teoremom o kretanju težišta:

                                                      (4.1)

 je masa segmenta, ubrzanje težišta, a  ubrzanje Zemljine teže.

Posmatrajmo sada obrtanje tela oko svog težišta. Položaj težišta na telu i u odnosu na zglobove prikazan je na slici 4.2b i definisan vektorimaikako je već objašnjeno u poglavlju o geometriji robota (odeljak 2.2.4). Obrtanje opisujemo Ojlerovom vektorskom jednačinom:

(4.2)

 je ugaono ubrzanje, a ugaona brzina segmenta. Oznake ~ ukazuje da su vektori izraženi trima projekcijama na koordinatnom sistemu vezanom za segment.

 je tenzor inercije sračunat za ose vezanog sistema. U opštem slučaju je

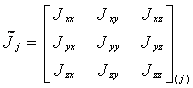             (4.3)

Međutim, ose vezanog sistema se najčešće postavljaju u pravcima glavnih osa inercije tela. Tada tenzor inercija ima dijagonalnu formu

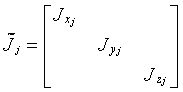          (4.4)

gde  predstavlja moment inercije oko ose vezanog sistema, a analogno važi za  i .Na desnoj strani jednačine (4.2) nalaze se momenti koji su takođe izraženi u odnosu na vezani sistem segmenta "j".Dogovor o korišćenju indeksa ~ iznad ili ispod oznake neke veličine ( npr.  i ) objašnjen je u odeljku 2.2.4. Treba naglasiti da je jednačinu (4.1) isto tako moguće napisati u vezanom sistemu čime bi se postigla jednoobraznost. Druga mogućnost je da se obe jednačine pišu u spoljašnjem sistemu. Tada (4.1) ostaje u obliku kakvom je već napisana, a (4.2) se prevodi u spoljašnji sistem množenjem sa prelaznom matricom .

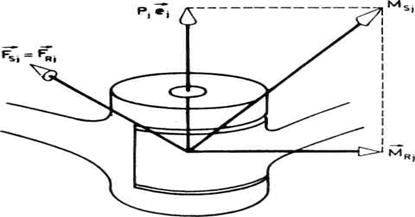
Sl. 4.3. Sila  i momenti u rotacionom zglobu

U izvedenim vektorskim jednačinama (4.1) i (4.2) pojavljuju se sila  i momenat , tj. ukupna sila i momenat u zglobu. Razmotrimo detaljnije ove veličine. Posmatrajmo prvo rotacioni zglob (sl. 4.3). Takav zglob dozvoljava samo jedno relativno pomeranje i to obrtanje oko ose. Otuda sila reakcije  (od segmenta "j-1" na segment "j") može imati bilo koji pravac, dok reakcioni momenat  mora biti normalan na osu (tj. ). U rotacionom zglobu deluje još i pogonski momenat ; dakle deluje oko ose. Ukupna sila i momenat u zglobu su sada:

           (4.5a)

Ranije smo rekli da  predstavlja reakciju. Međutim, sada smo tu reakciju podelili na reakciju  koja je posledica samog kinematičkog para tj. konstrukcije zgloba i komponentu , koje potiče od pogona.

Ako je posmatrani zglob "j" translatorni (sl. 4.4) tada je sila reakcije  normalna na osu, a reakcioni momenat može biti bilo kog pravca. U zglobu deluje i pogonska sila duž ose translacije: . Ukupna sila i momenat su tada

    (4.5b)

Jednačine (4.5a) i (4.5b) možemo napisati na jedinstven način

    (4.6)

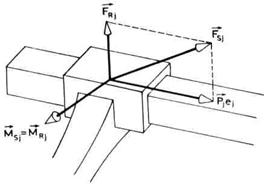
Sl. 4.4. Sile i momenat u  translatornom zglobu

uvođenjem indikatora , kojim određujemo tip zgloba (0 za rotacioni a 1 za translatorni zglob).Vektorske jednačine (4.1) i (4.2) zajedno sa (4.6) opisuju dinamiku segmenta "j". Ako ove jednačine napišemo za svaki segment dolazimo do 2n vektorskih jednačina:

      (4.7a)

        (4.7b)

koje opisuju dinamiku celog sistema.

U odeljku 2.3.2 (kinematika) pokazano je kako se ubrzanje težišta () i ugaona brzina i ubrzanje (,) mogu izraziti u zavisnosti od generalisanih koordinata q i njihovih izvoda  i . Ako to uradimo u sistemu (4.7) nakon toga nam preostaje da u sistemu izvršimo eliminisanje reakcija ,,j = l,...,n. Analizirajmo prvo broj jednačina i broj nepoznatih koje treba eliminisati. Sistem (4.7) sadrži 2n vektorskih, odnosno 6n skalarnih jednačina. Broj vektorskih reakcija koje treba eliminisati je takođe 2n tj. po dve u svakom zglobu. Međutim, broj nepoznatih skalarnih komponenata reakcija je 5n tj. po pet u svakom zglobu. To je zato što ona reakcija koja ima proizvoljan pravac sadrži tri nezavisne nepoznate skalarne komponente, a ona koja je normalna na osu zgloba sadrži dve. Sada, nakon eliminacije bn nepoznatih iz 6n jednačina dobija se sistem n skalarnih jednačina koje ne sadrže reakcije već samo skalarne vrednosti pogonskih sila i momenata (P₁,...,P_n).Postupaka za eliminisanje reakcija ima više i svaki od njih ima svoje specifičnosti. Otuda se razlikuju i po brzini rada i utrošku memorijskog prostora računara. Jedan metod za eliminaciju reakcija izložen je u prilogu P3.Bez obzira na izabrani pristup formiranju dinamičkog modela, kao razultat dobijamo sistem n skalarnih diferencijalnih jednačina drugog reda. Ovaj sistem, odnosno dinamički model može se napisati u obliku

     (4.8)

Označavanje  ukazuje da koeficijent  predstavlja funkciju generalisanih koordinata, a ukazuje da je sabirak  funkcija generalisanih koordinata q i brzina .

Sistem (4.8) može se napisati i u matričnom obliku

        (4.9)

gde su matrice sistema jednake:

       (4.10)

a matrica pogona:

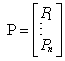k

Naglasimo još jednom  predstavlja pogonski momenat ako je  rotacioni zglob, a pogonsku silu ako je zglob translatorni. U svakom slučaju radi se o izlaznom momentu ili sili motora, a ako postoji reduktor tada se radi o izlaznom momentu reduktora. Ova diskusija je značajna jer možemo zaključiti da model (4.9) opisuje dinamiku mehanizma robota ne vodeći računa o dinamici pogonskih motora. Problem kod ovakvog modela nije samo u njegovoj teorijskoj nekompletnosti. Važniji je problem u korišćenju modela. Izlazni momenti motora ne mogu se menjati po želji i nezavisno jer to nisu ulazne upravljačke veličine već izlazne veličine koje zavise od ponašanja, odnosno dinamike motora. Ono što možemo po želji menjati to su ulazni naponi  u slučaju elektromotora i struje servorazvodnika u slučaju hidrauličnih motora. Promenom ovih upravljačkih veličina treba ostvariti željeno kretanje robota.Da bi se dobio dinamički model koji bi vodio računa o kompletnoj dinamici robotskog sistema potrebno je uz model (4.9) uzeti u obzir i matematičke modele pogonskih motora, kao i relacije koje pokazuju transformaciju momenata i brzina kroz reduktore (vidi glavu 3).O ovakvom kompletnom dinamičkom modelu biće reči nešto kasnije (4.3).Razmotrićemo sada podatke koje je potrebno poznavati da bi se mogao formirati dinamički model robota. Prvo, pošto je neophodno rešiti kinematiku robota, to je potrebno poznavati sve podatke o geometriji kao što je objašnjeno u glavi 2. Podsetimo sada da pod poznatom geometrijom podrazumevamo poznavanje ,za svaki segment "j". Svakako, potrebno je znati i tipove zglobova tj. indikatore , j=l,...,n. Za rešavanje dinamike robota potrebno je poznavati još i inercijalna svojstva segmenata: masu i tenzor inercije , za svaki segment "j". Nabrojani podaci predstavljaju karakteristike samog mehanizma i ne zavise od njegovog kretanja. Da bismo mogli praktično rešiti bilo direktni bilo inverzni problem dinamike moramo poznavati i početno stanje sistema tj. početni položaj q(t₀) i početnu brzinu (t₀).

4.2. DIREKTNI I INVERZNI PROBLEM DINAMIKE

U delu o kinematici uvedeni su pojmovi direktnog i inverznog problema kine-matike. Ovi pojmovi su bili vezani za izražavanje kretanja robota preko unutrašnjih i preko spoljašnjih koordinata, dakle uvedeni su specijalno za probleme robotike. U dinamici srećemo pojmove direktnog i inverznog problema dinamike, ali ti pojmovi nisu nužno vezani za robotiku, već se koriste u slučaju bilo kog mehaničkog sistema. Te pojmove ćemo zato i definisati za proizvoljan mehanički sistem. Ako posmatramo sistem tela koja se kreću pod dejstvom određenih sila, tada pod direktnim problemom podrazumevamo nalaženje sila koje izazivaju neko zadato kretanje sistema. Kod inverznog problema sile posmatramo kao poznate (zadate) i tražimo kretanje koje će one izazvati. U robotici, sistem koji posmatramo predstavlja mehanizam robota i on se kreće pod dejstvom težine i pogonskih sila i momenata. Kako su težine uvek poznate, to kada govorimo o zadatim silama ili traženju sila mislimo na sile i momente pogonskih motora, Formulisaćemo problem preciznije. Pod kretanjem robota podrazumevaćemo promenu unutrašnjih koordinata, dakle vremensku funkciju q(t). Pod poznatim pogonima podrazumevaćemo vremensku funkciju P(t). Sada pod direktnim problemom podrazumevamo nalaženje funkcije P(t) za poznato q(t), a pod inverznim problemima podrazumevamo nalaženje funkcije q(t) za poznato P(t).Razmotrimo rešavanje direktnog problema. Prvo ćemo uočiti osnovnu ideju za proračun. Ako je poznato kretanje q(t), onda možemo reći da su poznati i izvodi, odnosno unutrašnje brzine q(t) i unutrašnja ubrzanja q(t). Tada se pogoni mogu dobiti iz relacije (4.9).

      (4.12)

Pošto se ova ideja realizuje pomoću računara, to stvari stoje nešto drukčije. Funkcija q(t) nije data analitički već diskretizovano, odnosno nizom vrednosti koje odgovaraju nizu trenutaka vremena t₀,t₁,..., t_k. Neka je interval između pojedinih trenutaka jednak Δt. Kako relacija (4.12) zahteva poznavanje i,to bi bilo neophodno sprovesti numeričko diferenciranje, a to je nepoželjan posao. U delu 2.3.4 o direktnom i inverznom problemu kinematike pokazali smo da se numeričko diferenciranje može izbeći tako što ćemo kretanje zadati u obliku početnog stanja q(t₀), (t₀) i vremenske promene ubrzanja (t). Ako primenimo sličnu ideju, tada će shema rešavanja direktnog problema dinamike izgledati kao na slici 4.5a.

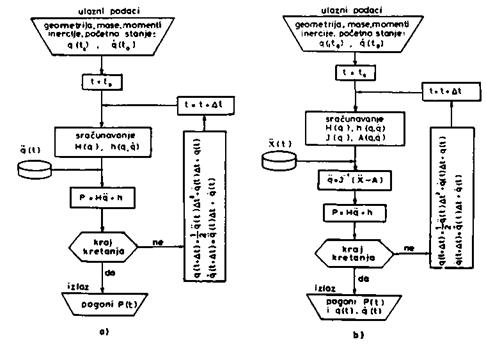
Sl. 4.5. Shema rešavanja direktnog problema  dinamike

U opisanom postupku rešavanja direktnog problema smatrali smo da je kretanje zadato preko unutrašnjih koordinata q(t) ili preciznije preko unutrašnjih ubrzanja (t). U teoriji kinematike robota (glava 2) ističe se da je kretanje pogodnije zadati preko spoljašnjih koordinata X(t). Tada se rešavanje direktnog problema dinamike mora kombinovati sa rešavanjem inverznog problema kinematike (sl. 4.5b).

Razmotrićemo sada rešavanje inverznog problema dinamike. On podrazumeva nalaženje kretanja q(t) ili X(t) ako je poznat zakon promene pogona P(t). U stvari, potrebno je izvršiti integraciju sistema diferencijalnih jednačina (4.9). Jedan jednostavni postupak integracije predstavljen je na slici 4.6 i zasnovan je na ideji da se ubrzanja smatraju konstantnim na malom intervalu Δt. Druga mogućnost je da se sistem 4.9 napiše u obliku

  (4.13)

koji je pogodan za upotrebu bilo koje od standardnih metoda za numeričku integraciju sistema diferencijalnih jednačina.

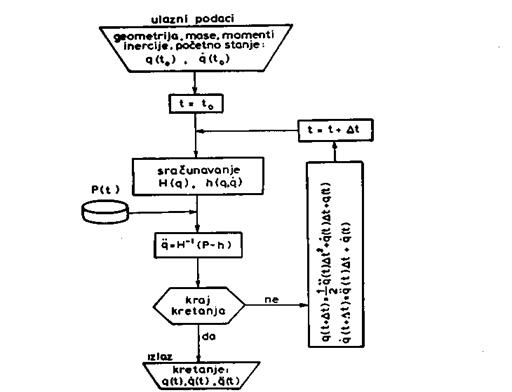
Sl. 4.6. Shema  rešavanja inveiznog problemu dinamike

Korištenjem bilo kog od spomenuta dva pristupa, dobijamo  zakon kretanja u unutrašnjim koordinatama q(t), unutrašnje brzine(t) i ubrzanja(t). Dobijene funkcije su, naravno, diskretizovane. Ako želimo da nađemo kretanje u spoljašnjim koordinatama onda je potrebno rešiti još i direktni problem kinematike.

 4.3. KOMPLETAN MODEL DINAMIKE ROBOTA

U odeljku 4.1 naglasili smo da izvedeni dinamički model (4.9) ne opisuje kompletnu dinamiku robota. Naime, izveli smo model za mehanizam robota, a nismo uključili dinamiku pogonskih motora. Sada ćemo izvesti kompletan dinamički model koji povezuje upravljačke veličine (napon kod motora jednosmerne struje i struja servorazvodnika kod hidrauličnog motora) sa kretanjem robota (q(t)).U principu, kompletan dinamički model određenje modelom mehanizma (4.9) kome se pridružuju modeli motora. Tako, ako se robot pokreće elektromotorima jednosmerne struje, tada modelu (4.9) pridružujemo model (3.8) za svaki zglob j=l,...,n. Takođe, potrebno je definisati vezu koordinata obrtanja motora () i koordinata pomeranja zgloba (), dakle prenosni sistem, a zatim i promenu momenta kroz taj prenos. U odeljku 3.2.3 izveli smo transformaciju kretanja i pogona kroz prenosni sistem sa reduktorom što je opisano relacijama (3.13)-(3.15), j=l,...,n. Ukupno, dinamiku robota opisujemo jednačinama:

                                          (4.14)

za mehanizam,

                      (4.15a)

      (4.15b)

za  pogonske motore (aktuatori) i

   (4.16a)

     j=1,...,n                                                 (4.16b)

za prenosni sistem (transmisija).

Naglasimo da model SA može biti i nižeg reda, na primer, drugog reda kao što je dato relacijom (3.12). Naglasimo takođe da linearnost relacije (4.15a) po naponu  važi samo do određene granične vrednosti. U opštem slučaju, umesto u pisali bismo funkciju n() koja predstavlja nelinearnost tipa zasićenja. Konačno, recimo još da prenos pogona uvek unosi gubitke, što obično izražavamo kroz koeficijent korisnog dejstva (relacija (3.17)).Ako se robot pokreće hidrauličnim pogonom tada modelu mehanizma (4.9) pridružujemo model (3.20)-(3.23) ili model (3.27). Prenos pogona ovde može biti prilično raznolik. Kod obrtnih motora veza se može svesti na oblik (3.13) - (3.15) odnosno na (4.16). Međutim, kod hidrauličnog cilindra veza između pomeranja klipa () i pomeranja zgloba () može biti direktna ( = ) ali može biti i posredna: linearna ( = r) ili nelinearna ( = f()). Slično važi i za odnos momenata.

Razmotrimo sada mogućnost da se ukupni dinamički model napiše u kompaktnoj formi. Smatraćemo da se model svakog pogonskog sistema može uz određena uprošćenja linearizovati i opisati jednačinom (4.15a). Red modela tj. dimenzija vektora  neka je , a vektor sadrži određene promenljive koje definišu stanje sistema.  predstavlja upravljačku promenljivu koja odgovara posmatranom pogonskom sistemu, a  izlazni pogon (momenat ili sila). Dalje, radi jednostavnosti izvođenja pretpostavimo direktnu vezu pomeranja motora i pomeranja zgloba (= 1 u (4.16)) što ne umanjuje opštost jer se prenosni odnos lako može ugraditi u model.

Sledeći relaciju (4.13), model mehanizma SM napišemo u obliku

       (4.17)

gde je  = q,  = . je kolona vektor stanja mehanizma i dimenzija mu je 2n(4.17) se dalje može napisati u obliku

      (4.18)

gde je

            (4.19)

Posmatrajmo ponovo motore. Neka se  elemenata vektora  poklapa sa elementima vektora ξ tj.  koordinata stanja motora "j" je već sadržano u vektoru stanja mehanizma. Na primer, obrtanje motora () i brzina  se po pretpostavci poklapaju sa  i  i uključeni su u ξ. Tada bi bilo

 i k

popunjen ceo vektor ξ.

Napišimo sada model SA tj. (4.15a) u kompaktnoj formi:

                                           (4.20)

gde je kolona vektor stanja  dimenzije . Dalje je , C=diag[C1...Cn],  F = diag[], D = diag[]. Uočimo da je ceo vektor ξ uključen u  pa  definiše ukupno stanje robota. Ujedinimo sada modele SM i SA tj (4.14) i (4.20). Uvedimo prvo matricu  dimenzije 1 x  takvu da je. Na primer, ako je  određeno sa (4.15b) i  Sada iz (4.14) sledi

 (4.21)

gde je T=diag [Ti...rn]. Zamenom x iz (4.20) i (4.21) dobija se

                            (4.22)

gde je E_n jedinična matrica dimenzije n x n. Zamenimo sada P iz (4.22) u (4.20). Čime dobijamo kompletni model dinamike robota u obliku

                                                           (4.23)

Matrice sistema su

                                       (4.24)

i dimenzije su im N l i Nn respektivno.

Očigledno da sada pojam direktnog i inverznog problema dinamike treba preformulisati. Direktni problem podrazumeva nalaženje upravljanja u (t) koje je potrebno da bi se ostvarilo zadato kretanje robota, a inverzni problem podrazumeva nalaženje kretanja ukoliko je poznato upravljanje. Ovo drugo nazivamo simulacijom.

4.4. PRIMENA RAČUNARA ZA PRORAČUN DINAMIKE

Iz dosadašnjeg izlaganja o formiranju matematičkog modela dinamike robota možemo zaključiti da se teško može izvršiti ručno sastavljanje takvog modela. Ovaj zaključak trebalo bi obrazložiti. Postupak za formiranje diferencijalnih jednačina kretanja omogućava, u principu, da se jednačine napišu ručno. Međutim, takav pristup ima mnogo nedostataka. Prvo, jako je velika mogućnost grešaka pri tako složenom izvođenju. Drugo, ako se matematički model i formira bez greške, on će biti veoma kabast i nepodesan za upotrebu. Iste mane pojaviće se ako se za ručno formiranje modela izabere bilo koji drugi mehanički pristup. Otuda se javlja ideja da se ceo taj složeni posao formiranja i rešavanja matematičkog modela robota prebaci na računar. Postupak za formiranje matematičkog modela formuliše se tako da ima rekurzivni karakter, te je veoma prikladan za primenu na računaru (vidi prilog P3). Objasnimo sada ideju primene računara za rešavanje dinamike.

Posmatrajmo matematički model (4.9). Matrice modela H(q) i h( q,) mogu se posmatrati kao analitički izrazi koji određuju zavisnost od q, odnosno od q i . S druge strane možemo H(q) i h(q, ) tretirati kao složene računarske postupke kojima se izračunava brojna vrednost H polazeći od brojno poznatog q i, takođe, brojna vrednost h, polazeći od q i . Tako, kompletne analitičke izraze za matematički model na ovaj način nećemo dobiti, ali postupci za brojno sračunavanje matrica modela dovoljni su za rešavanje direktnog i inverznog problema dinamike. Prvi računarski postupci za proračun dinamike bili su zasnovani na ovakvom postupku. Oni su omogućili Siru primenu računara u robotici.

Opisani numerički pristup ima i svoje nedostatke. Sheme na slikama 4.5 i 4.6 pokazuju da je sračunavanje matrica H i h neophodno izvršiti ponovo kada god se promene vrednosti q i , dakle u svakom koraku integracije. Pri takvom računu svaki put će se iznova sračunavati i mnoge veličine koje ne zavise od q i  i koje se nisu menjale. Očigledno, ponešto će se nepotrebno računati jer se moglo izračunati samo jednom, na početku. U svakom slučaju, opisani numerički pristup ne omogućava da se u proračunu izdvoje ti elementi koji ne zavise od q i  od onih koji zavise i koji se moraju računati za svaki trenutak vremena ponovo. Zato se došlo na ideju da se odustane od numeričkog modela i da se vrati na analitičke izraze H(q) i h(q, ). Ovo lici na povratak ručnom pisanju modela, međutim, u ovom novom pristupu analitičke izraze sastavlja računar. U dobijenim izrazima lako se izdvajaju elementi koji ne zavise od q i  i koji se mogu izračunati samo jednom, na početku. Ovakav pristup se obično naziva simboličkim modelom.Računarski postupci za formiranje i rešavanje dinamičkog modela omogućili su da se konačno sretnu teorija i praksa robotike. Do tada, teorija se razvijala pretežno akademski, bez ozbiljnije primene, a praksa je napredovala nezavisno, oslanjajući se na znanja iz oblasti automatskog upravljanja. Jasno je da je takva praksa imala svoje granice preko kojih nije mogla preći bez celovitije teorije robota. Primena računara za rešavanje kinematike i dinamike omogućila je da se prevaziđu nedostaci teorije robotike i ona postane upotrebljiva u praksi.Ovakva, računarski orijentisana kinematika i dinamika iskorisćene su s jedne strane za razradu savršenijih metoda upravljanja robotima, a s druge strane za razvoj metoda računarskog projektovanja robota. Kako ćemo se upravljanjem baviti u posebnoj glavi ove knjige, to ćemo ovde obratiti pažnju na mogućnosti primene dinamike i računara u procesu projektovanja mehanizma i pogonskog sistema robota.

U odeljku 4.2 opisan je računarski postupak za rešavanje direktnog problema dinamike. Postupak omogućava da se, polazeći od željenog kretanja izraženog preko spoljašnjih koordinata X(t), izračuna promena unutrašnjih koordinata q(t), brzina (t) kao i potrebni pogonski momenti P(t). Ovi podaci već sami po sebi mogu biti korisni, a na osnovu jednačina koje opisuju kinematiku i dinamiku robota moguće je izračunati i niz drugih karakteristika. Moguće je odrediti sve reakcije u zglobovima, a zatim za svaki od segmenata naći raspodelu sila koje na njega deluju. Odatle se dobijaju mehanički naponi u materijalu (npr. naponi savijanja i uvijanja). Sledeći korak je proračun elastičnih deformacija. Proračun deformacija može biti uprošćen jer bi egzaktno tretiranje zbog tog problema vodilo ka elastodinamici koju najčešće moramo rešavati primenom metode konačnih elemenata. U svakom slučaju proračun napona i deformacija služiće nam kao osnova za projektovanje dimenzija robota.Proračunom dinamike robota dobija se niz karakteristika potrebnih za izbor pogonskih motora. Pored potrebnih momenata i brzina lako možemo sračunati potrebnu snagu, a takođe formirati dijagram brzina-momenat (P-). Ovakav dijagram može se uporedivati sa kataloškim karakteristikama motora. Na opisani model dinamike robota lako se dodaje modul za proračun grejanja i prenosa toplote u motorima.Moguće je izračunati još neke dinamičke karakteristike kao što je utrošak energije itd. Tako dolazimo do zaključka da raspolažemo postupkom koji omogućava da se zada željena konfiguracija robota (dimenzije, mase, itd.) i željeni manipu-lacioni zadatak, a kasnije izračuna niz dinamičkih karakteristika. Takav postupak nazivamo algoritmom za dinamičku analizu. Ovaj algoritam, u vidu računarskog programa, predstavlja korisnu alatku u procesu projektovanja robota. Projektant može brzo proanalizirati veći broj različitih konfiguracija robota radi izbora najpovoljnije. Može i menjati pojedine dimenzije i druge parametre da bi uočio uticaj tih promena na važne dinamičke karakteristike. Sve ovo omogućava brže i uspešnije projektovanja.Sledeći korak u korišćenju računara za projektovanje robota je formiranje takozvanog interaktivnog postupka projektovanja i odgovarajućeg programskog pa-keca. Cilj nam je da za postavljeni manipulacioni zadatak odaberemo konfiguraciju robota (dimenzije, motore itd.) koja će zadovoljiti sve postavljene zahteve i sva ograničenja. Kao prime ograničenja možemo navesti uslov da elastična deformacija segmenata robota bude manja od dozvoljene vrednosti. Shema programa prikazana je na slici 4.7. Postupak kreće od neke zadate početne konfiguracije robora. Izvrši se dinamička analiza i testiranje izračunatih dinamičkih karakteristika. Ukoliko su svi testovi pozitivni, dakle sva ograničenja zadovoljena, onda je posmatrana konfigracija dobra. Ako pak neki test bude negativan, dakle neko od ograničenja ne bude zadovoljeno, računar će štampati odgovarajuću poruku kao i preporuke za izmene konfiguracije koje će popraviti negativni test. Programski paket sadrži i posebne konunikacione potprograme koji omogućavaju projektantu jednostavnu izmenu pojedinih podataka o konfiguraciji robota. Nakon što je projektant uveo korekcije konfiguracije, postupak kreće od početka tj. vrši novu dinamičku analizu i testiranje. Takav ciklus se ponavlja sve dok se konačno ne dođe do konfiguracije koja zadovoljava sve zahteve i sva ograničenja, a to će biti onda kada svi testovi budu pozitivni.

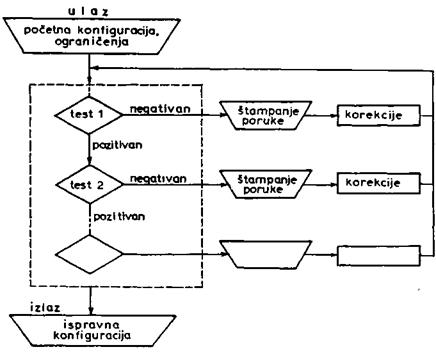
Sl. 4.7. Algoritam za  interaktivno projektovanje

Krajnji korak u korišćenju računara u projektovanju robota je formiranje postupka i programskog paketa koji bi na osnovu postavljenih zahteva vršio automatski izbor najpovoljnije konfiguracije robota. Ovaj postupak podrazumeva definisanje nekog kriterijuma optimalnosti i razvoj pogodnih metoda optimizacije.

Ovim bismo zaključili naše izlaganje ideja računarskog projektovanja u robo-tici. Opisane postupke dopunjavamo i programima za simulaciju i grafičko prikazivanje čime kompletiramo programski paket za računarsko projektovanje.

4.5. DINAMIKA ROBOTA SA OGRANIČENIM KRETANJEM HVATALJKE

Ovaj odeljak obrađuje dinamiku robota čija hvataljka ne može da se kreće proizvoljno u prostoru, već su joj nametnute određena ograničenja. Pri ovome naglasimo da pod terminom hvataljka podrazumevamo poslednji segment lanca bez obzira na završni uređaj koji se tu nalazi. Ovakva ograničenja nametnuta kretanju hvataljke česta su u nekim fazama izvršenja robotskog zadatka. Na primer, ako robot treba da piše po nekoj površini (sl. 4.9) tada hvataljka ne može da se kreće proizvoljno već se vrh pisaljke prinudno kreće po površini. Drugi primer bi se mogao naći u zadacima montaže (sl. 4.10 i 4.11). Ako, robot uvlači neki predmet u otvor tada je kretanje poslednjeg segmenta (koji u sebe uključuje i predmet) ograničeno na jednu translaciju i eventualno jedno obrtanje. Konačno, ograničenja se javljaju i u slučajevima dvoručne ili višeručne manipulacije (sl. 4.12). Niz drugih primera mogao bi se navesti. U svakom slučaju jesno je da uvedena ograničenja smanjuju broj stepeni slobode hvataljke, a takođe, ograničenja izazivaju pojavu sila reakcije veze koje bitno utiču na dinamiku robota. Ovde ćemo problem tretirati tako da pokrijemo one slučajeve koji su interesantni za praktičnu primenu.

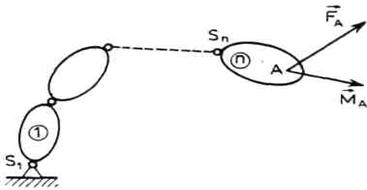
Sl. 4.8. Mehanizam robota sa silom i momentom

Posmatrajmo radi uprošćenja robot sa n = 6 stepeni slobode i smatrajmo da tokom izvršenja za dataka robot ne dolazi u singularne položaje. U tom slučaju, bez uvedenih ograničenja hvataljke bi takođe imala 6 stepeni slobode. Dinamiku ovakvog mehanizma možemo opisati modelom (4.9). Radi daljeg izvođenja proširimo posmatranje na robota na čiji poslednji segment, u zadatoj tački A, deluje sila  i još deluje spreg momenta   (Sl.4.8) koji deluju na hvataljku Tačka A definisana je vektorom . Dinamiku ovakvog mehanizma opisujemo modelom:

     (4.25)

gde je FA matrica dimenzija 31 koja sadrži elemente vektora , matrica MA (takođe 31) sadrži vektor  (dakle zadržavamo dogovor o pisanju vektora u obliku 31 matrice i obrnuto). DF i DM su odgovarajuće matrice dimenzija n3 koje pokazuju uticaj  i  na generalisane sile u zglobovima:

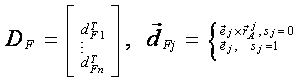                 (4.26)

                          (4.27)

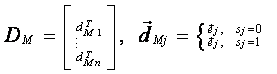                       (4.28)

Pri posmatranju kretanja sa ograničenjem, FA i MA će predstavljati reakcije ograničenja (reakcije veze). U praksi se uvođenje ograničenja najčešće svodi na kontakt hvataljke sa nepomičnom podlogom (stacionarno ograničenje) ili pak na kontakt sa nekim telom koje se kreće po zadatim zakonima i na čije kretanje robot ne utiče (nestacionarno ograničenje). Ipak, javljaju se i slučajevi kada dinamika robota utiče i na tela sa kojima je robot u kontaktu (na primer, dvoručna manipulacija). U svakom slučaju, dobija se struktura zatvorenog lanca.

4.5.1. Opšta metodologija uvođenja ograničenja

U poglavlju o kinematici uveden je vektor spoljašnjih koordinata koji, u slučaju n- 6, sadrži sledeće komponente.

     (4.29)

Ovaj vektor povezan je sa unutrašnjim koordinatama preko Jakobijeve forme (2.56):

   (4.30)

Ako uvedemo ograničenje na kretanje hvataljke tada će se smanjiti broj stepeni slobode. Neka je ,ovaj smanjeni broj.Obično govorimo o redukovanom broju stepeni slobode hvataljke. Dakle, posmatramo ograničenje koje ukida  stepeni slobode pri čemu je  = n-. Za definisanje položaja hvataljke sada uvodimo  nezavisnih parametara  koji formiraju takozvani redukovani vektor položaja

                           (4.31)

Najčešće se parametri  uvode tako da određuju relativni položaj hvataljke u odnosu na uvedeno ograničenje. Vektor spoljašnjih koordinata X moguće je povezati sa redukovanim vektorom položaja  preko nove Jakobijeve forme

                             (4.32)

gde je J_r takozvani redukovani jakobijan dimenzija n×nr, pridružena matrica Ar je dimenzija  n×1. Matrice J_r i A_r izvode se iz relacija koje definišu postavljeno ograničenje.

Kombinovanjem (4.30) i (4.32) dobija se

                          (4.33)

Ova relacija definiše kinematiku ograničenog kretanja. Dinamiku ograničenog kretanja opisujemo modelom (4.25) pri čemu i predstavljaju silu reakcije veze i reakcioni momenat.   Model možemo napisati i kompaktnije:

                                        (4.34)

   gde je

                                       (4.35)

  šestokomponentni vektor reakcije, a

                                          (4.36)

je dimenzija n × 6.  Komponente vektora reakcije R_A u opštem slučaju nisu nezavisne, već u zavisnosti od tipa uvedenog ograničenja zadovoljavaju određene međusobne odnose koji se mogu izraziti relacijom

                                           (4.37)

gde je E matrica dimenzija (6 - n + nr) ×6, koja se izvodi iz izraza koji definišu uvedeno ograničenje. Sada relacije (4.33), (4.34) i (4.37) definišu matematički model kinematike i dinamike ograničenog kretanja mehanizma robota. Ako želimo kompaktniju formu modela zamenićemo  iz (4.33) u (4.34) i dobiti

               (4.38)

Sada ovu realizaciju, zajedno sa (4.37) možemo napisati u obliku:

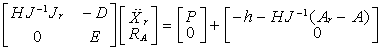 (4.39)

Dobijeni model je dimenzije (n_r + 6) × (n_r + 6). Moguće je, međutim, napisati još kompaktniju formu. Šestokomponentni vektor reakcije R_A može se izraziti kao linearna funkcija n_c nezavisnih komponenata. Dakle, nezavisnih komponenata ima n_c = n-n_r, odnosno onoliko koliko stepeni slobode je "ukinuto" uvođenjem ograničenja. Sada  je

          (4.40)

gde R_Ar vektor dimenzije n- n_r koji sadrži nezavisne reakcije i koji nazivamo još redukovani vektor reakcije. Matrica G dimenzija (6 ×(n — n_r)) izvodi se polazeći od definicionih relacija ograničenja. Uvođenjem (4.40) u (4.38) dobija se dinamički model

             (4.41)

odnosno

      (4.42)

Dimenzije blokova u ovom modelu su:

           (4.43)

pa je model dimenzija (n × n).

Razmotrimo prvo rešavanje direktnog problema dinamike. Pod tim terminom ćemo ovde podrazumevati da je zadato kretanje X_r(t) i reakcije R_Ar(t) koje želimo ostvariti, a traže se odgovarajući pogoni u zglobovima P(t). Očigledno, P se izračunava direktno iz jednačine (4.42).

Inverzni problem podrazumeva integraciju modela. Zadati su pogoni P(t), a traži se kretanje X_r(t) i reakcija R_Ar (t). Model (4.42) omogućava rešavanje ubrzanja  i reakcija R_Ar, a time i integraciju modela.

4.5.2. Tipovi ograničenja

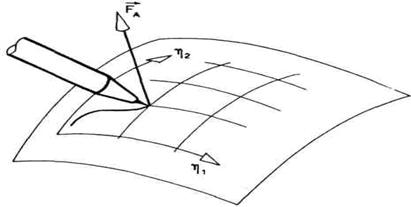
Sl. 4.9. Zadatak pisanja - ograničenje tipa površine

Razmotrimo tipove ograničenja koji se javljaju u praktičnim problemima. Ovde ćemo glavne tipove ukratko objasniti, a u prilogu P4 izvešćemo dinamički model tj. matrice J_r, A_r, E i G, Za jedan konkretan tip ograničenja - ograničenje u obliku površine.

Jedno od čestih ograničenja je ograničenje tipa površine (sl. 4.9). Tada je položaj hvataljke određen sa dva relativna parametra  i  koji definišu položaj vrha pisaljke na površini i tri ugla koji definišu orijentaciju hvataljke. Uvedeno ograničenje ukinuto je jedan stepen slobode (n_c= 1). Redukovani vektor položaja ima komponente X_r = i dimenzije je n_r = 5. Sto se tiče reakcija, momenat je jednak nuli ( = 0), a sila reakcije  mora biti normalna na površinu (podrazumevajući glatku površinu), pa ima jednu nezavisnu komponentu (n_c = n-n_r = 1).

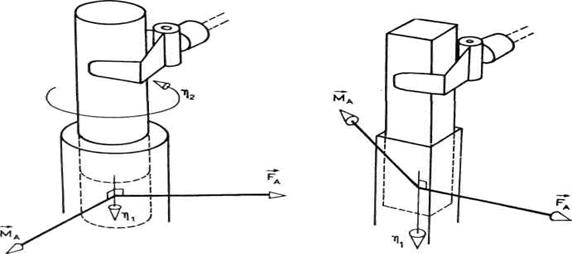
Sl.4.10.Zadatak montaže - ograničenje tipa cilindričnog para          Sl.4.11.Zadatak montaže - ograničenje tipa translatornog para

Drugi čest slučaj ograničenja je ograničenje tipa cilindričnog para (sl. 4.10). Tada hvataljka ima samo dva stepena slobode (n_r = 2) jer je moguća samo translacija duž ose otvora i obrtanje oko te ose. Tim pomeranjima odgovaraju parametri »7i i »72 koji čine redukovani vektor položaja: X_r = []T. Reakcije  i  moraju biti obe normalne na osu otvora, pa, prema tome, svaka od njih ima po dve nezavisne komponente. Dakle, n_c = n- n_r = 4.

U procesu montaže javlja se i ograničenje tipa translatornog para (sl. 4.11). Za razliku od prethodnog slučaja, ovde hvataljka ima samo jedan stepen slobode (uvlačenje) pa je n_r = 1 i redukovani vektor položaja sadrži samo podužnu koordinatu uvlačenja: Xr = []. Sila reakcije  je i dalje normalna na osu otvora, pa ima dve nezavisne komponente, ali, reakcioni momenat  može imati proizvoljan pravac, pa ima tri nezavisne komponente.   Dakle, ukupno ima n_c = n - n_r = 5 nezavisnih komponenata reakcije.

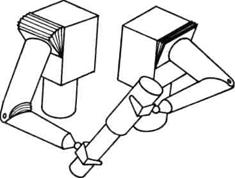
Sl. 4.12. Dvoručna  manipulacija

Još niz tipova ograničenja možemo nabrojati, međutim, ovde ćemo spomenuti još samo jedan specijalan slučajdvoručnu manipulaciju. Na slici 4.12 prikazana su dva robota koji obavljaju zadatak montaže. Tokom izvršenja zadataka njihove hvataljke su povezane cilindričnim parom.Kada govorimo o kretanju robota sa ograničenjem nametnutim na kretanje hvataljke, neophodno je spomenuti i pitanje sudara. Naime, pri nailasku na ograničenje tj. pri pre      lasku sa slobodnog na ograničeno kretanje dolazi do sudarnog efekta. Sudar se, u opštem slučaju, rešava primenom

teoreme o količini kretanja i teoreme o kinetičkom momentu (vidi prilog P4). Jedan slučaj kretanja robota sa ograničenjem obrađen je i prilogom na kraju knjige.

4.6.DINAMIKA ROBOTA SA ELASTIČNIM PRENOSOM POGONA

U odeljku 3.2.3 gde je govoreno o prenosu pogonskog momenta od motora do zgloba videli smo da se često projektuje prilično složen prenosni sistem i da se često pogonski momenat prenosi na relativno veliku daljinu. Obično se radilo o prenosu osovinom ili lancem, a skoro uvek je u prenosni sistem uključen reduktor.

Pri pisanju relacija kojima opisujemo prenosni sistem smatralo se da je takav sistem nedeformabilan. Tako se došlo do relacija (3.13) - (3.15) koje su korišćene i kasnije u dinamici (relacija (4.16). Dakle, obrtanje zgloba (q_j) direktno je sledilo iz obrtanja motora (). Međutim, prenosni sistem nikada ne može biti u potpunosti krut. Naime, uvek postoje elastične deformacije, pa možemo reći da je relacija (4.16) aproksimativna i da važi tek za dovoljno krut prenos. Sada se postavlja pitanje šta znači "dovoljno krut" prenos. Mehanička krutost elemenata prenosnog sistema jeste velika i najčešće je aproksimacija (4.16) opravdana. Međutim, u nekim preciznim proračunima deformacije u prenosu se moraju uzeti u obzir. Uzmimo na primer deformaciju istezanja prenosnog lanca ili deformaciju uvijanja cevastog dela harmonik-drajv reduktora. Zato ovde pokazujemo, na nešto uprošćenom primeru, kako izgleda dinamički model robota sa elastičnim prenosnim sistemom. Na sličan način može se analizirati i prenos sa složenijom elastičnom deformacijom tj. sa više deformabilnih elemenata. Kako se radi i o dinamici motora i o dinamici mehanizma, to će dobijeni model predstavljati kompletni model dinamike. Prilikom izvođenja kompletnog dinamičkog modela (odeljak 4.3) opisali smo mehanizam modelom (4.14), motore modelom (4.15), a prenosni sistem relacijama (4.16a) i (4.16b). U slučaju deformabilnog elastičnog prenosa modeli mehanizma i motora se ne menjaju. Menjaju se, međutim, relacije koje opisuju prenos. Neka je prenosni sistem takav kakav je prikazan na slici 4.13. i neka je jedini elastični elemenat osovina A_j'A_j''. Konstantu torzione krutosti označimo sa , a konstantu prigušenja sa .

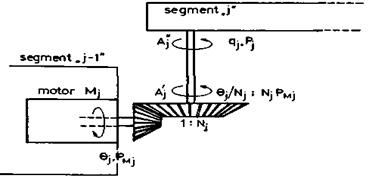
Sl. 4.13.  Uprošćeni sistem za prenos pogona

Moment motora  predstavlja ulazni momenat za zupčast par. Nakon zupčastog para (zanemarujući njegovu inerciju) dobija se momenat koji se osovinom A_j'A_j" prenosi na zglob. Ako se zanemari inercija osovine onda je

               (4.44)

tj. relacija (4.16a) važi i u slučaju elastičnog prenosa. Međutim, usled elastične deformacije osovine A_j'A_j'' koordinata obrtanja motorai koordinata obrtanja zgloba postaju međusobno nezavisne. Time se broj generalisanih koordinata povećava za n( ,j = l,...,n), a broj promenljivih stanja za 2n(,, j = 1...., n).

Relacija (4.16b) očigledno više ne vazi, jer se pojavljuje uvijanje tj. ugaona deformacija . Relacija (4.16a) tj. (4.44), mada važi, ne primenjuje se u tom obliku. Momenat koji vrši elastičnu deformaciju može se napisati u obliku    

   (4.45)

Sada model mehanizma (4.14) postaje

                (4.46)

gde je

                              (4.47)

             (4.48)

Model motora (4.15) postaje

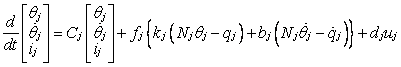         (4.49)

Sada (4.46) i (4.49) određuju kompletan model dinamike robota.   Ukupan broj koordinata stanja je 5n ( ,,j = l,...,n).